728x90
728x90
Binary Search(이진탐색)
정렬된 배열, 이진 트리에서 특정한 값을 찾아내는 알고리즘이다.

- 정렬이 전제되어 있어야 한다.
- 한번 비교를 거칠 때 탐색 범위가 1/2로 줄어든다.
- 범위의 중앙 값과 비교한다.
- 찾는 값이 중앙 값보다 작다면 왼쪽(그림 : 내림차순 정렬이므로 오른쪽) 1/2의 범위에서 탐색한다.
- 찾는 값이 중앙 값보다 크다면 오른쪽(그림 : 내림차순 정렬이므로 왼쪽) 1/2의 범위에서 탐색한다.
- 1번/2번 해당하는 작업을 반복한다.
- 찾는 값이 중앙 값이면 탐색을 종료한다.
기본 형태의 Java 코드
int BinarySearch(int dataArr[], int size, int findData)
{
int low = 0, high = size - 1, mid;
// high가 low보다 작아진다면 찾으려는 데이터가 데이터 집합에 없다.
while (low <= high)
{
// 중앙값은 low와 high를 더한 값을 2로 나누면 된다.
mid = (low + high) / 2;
// 만약 찾으려는 값이 중앙값보다 작다면 high를 mid - 1로 둔다.
if (dataArr[mid] > findData) high = mid - 1;
// 만약 찾으려는 값이 중앙값보다 크다면 low를 mid + 1로 둔다.
else if (dataArr[mid] < findData) low = mid + 1;
// 중앙값과 찾으려는 값이 일치하면 mid를 반환한다.
else return mid;
}
// 데이터를 찾지 못하면 -1를 반환한다.
return -1;
}
시간복잡도
전체 데이터의 크기를 n이라고 한다면
탐색 범위는 n 으로 시작하여 1/2로 변화한다.
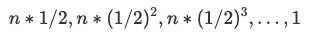
최악의 경우는 탐색 범위가 1일때까지 탐색한 경우다.
따라서, 탐색 횟수를 k라고 한다면 n * (1 / 2) ^ k = 1 을 만족하는 k가 시간복잡도가 된다.
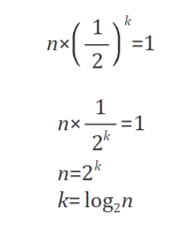
-> O(logn)의 시간복잡도를 가진다.
Lower Bound
원하는 값 k 이상이 처음 나오는 위치를 의미한다.
이분탐색 방법의 조건을 조금 수정한 알고리즘을 사용한다.
Java 코드
int lowerBound(int dataArr[], int size, int findData)
{
int low = 0, high = size - 1, mid;
// high가 low보다 같거나 작아지면 그 값이 Lower Bound 이다.
while (low < high)
{
// 중앙값은 low와 high를 더한 값을 2로 나누면 된다.
mid = (low + high) / 2;
// 만약 찾으려는 값이 중앙값보다 작다면 high를 mid로 둔다.
if (dataArr[mid] >= findData)
high = mid;
// 만약 찾으려는 값이 중앙값보다 크다면 low를 mid + 1로 둔다.
else
low = mid + 1;
}
// 데이터를 찾지 못하면 -1를 반환한다.
return high;
}
Upper Bound
원하는 값 k를 초과한 값이 처음 나오는 위치를 의미한다.
lower bound와 마찬가지로 이분탐색을 조금 수정한 알고리즘을 사용한다.
Java 코드
int upperBound(int dataArr[], int size, int findData)
{
int low = 0, high = size - 1, mid;
// high가 low보다 같거나 작아지면 그 값이 Lower Bound 이다.
while (low < high)
{
// 중앙값은 low와 high를 더한 값을 2로 나누면 된다.
mid = (low + high) / 2;
// 만약 찾으려는 값이 중앙값보다 크다면 high를 mid로 둔다.
if (dataArr[mid] > findData)
high = mid;
// 만약 찾으려는 값이 중앙값보다 작다면 low를 mid + 1로 둔다.
else
low = mid + 1;
}
return high;
}
추가 질문
Q. 이진탐색의 논리를 적용하여 삼진탐색을 작성한다고 가정한다면, 시간복잡도는 어떻게 변화할까요? (실제 존재하는 삼진탐색 알고리즘은 무시하세요!)
더보기
삼진 탐색 : 한 번 비교를 거칠 때 탐색 범위를 1/3로 줄이며 탐색할 수 있다.
- 최악의 경우에는 2개의 기준점을 모두 비교 하고 다음 범위로 넘어간다.
- 이진 탐색은 1번의 비교를 통해 탐색 범위를 1/2로 줄이고, 2번의 비교를 통해 탐색 범위를 1/4로 줄인다.
- 그러나, 삼진 탐색은 2번의 비교를 통해 탐색 범위를 1/3로 줄인다. (범위 재설정 : O(1) = 기준점과 비교 : O(1) 이므로)
- 따라서 단순한 삼진 탐색 알고리즘보다 이진 탐색 알고리즘이 더 빠르다.
참고
이진 탐색(binary search)
정렬되어 있는 요소들을 반씩 제외하며 찾는 알고리즘이다.반드시 정렬이 되어있어야 사용이 가능하다.배열 혹은 이진 트리를 이용하여 구현가능하다.O(log N)의 시간 복잡도를 가진다.이진 탐색
velog.io
728x90
728x90
'Computer Science > Algorithm' 카테고리의 다른 글
| 암호화 알고리즘 (1) | 2023.03.09 |
|---|---|
| MST(Minimum Spanning Tree, 최소 신장 트리) (0) | 2023.03.09 |
| 재귀함수(Recursion) (0) | 2023.03.09 |
| 그리디 알고리즘(Greedy Algorithm) & 동적 계획법(Dynamic Programming) (0) | 2023.03.09 |
